Last week I watched the movie "Arrival". In it, Aliens visit the Earth and in an attempt to communicate, the US government calls in a linguistics expert (Amy Adams). Adams' job is build a grammar and language from the alien "ink blot" method of communication. The crux of the story is premised on how learning a foreign language changes the way you think (to suit the language). I guess that's why it's currently popular for kids to learn multiple spoken languages from a young age.
Ever wonder why your programmer friend seems a little odd? I don't think it's because programmers are all inherently strange. As programmers we have to learn at least one foreign language, the language we are coding in, and in the process the way we think is altered. The more different languages we learn the more varied are the changes in our brain.
I don't just mean learning Java and C# (both object-oriented langauges). There are different types of languages, such as:
- Procedural languages, where code is written in the order it is executed. Procedural code is executed like reading a book.
- Functional lanauges, where code is written in small blocks of functions and each function is passed around (I've not really ever used a functional language so I can't give a good analogy for it)
- Object Oriented (OO) languages, where we coders think of things as related objects that have properties and methods. Such as a person is an object. A person has some properties like an age, a name, etc. Person also has methods such as run, walk, speak. Methods DO something. In an OO language we pass messages between objects. These messages act on other objects' properies and methods.
- Set Query Languages (like SQL). These set based query languages are popular with databases, which are just sets of data. When programming in this type of language you have to think in sets and operations on sets, like: filter (pick some items from a larger collection of items), sort (order items), project (pick a few properties from each item), union (merge sets together). Dealing in sets has it's mathematics and it's own way of thinking. (Set Theory).
One of the defining characteristics of computers is that they are (supposed to be) deterministic. That is, they will always do the same thing given the same program. Computers also operate on binary logic, that of Off and On, True or False.
One of the most common and basic constructs in programming is the conditional statement known as an "if" statement. IF logic is known as an implication (denoted =>) and is read "If p, do q", where Q is performed only when P is true (Q if and only if P). http://mathworld.wolfram.com/Implies.html
This kind of logic occurs all the time in programming. For example, when you're attempting to withdraw money from your bank account via the atm or EFTPOS. The software will do a logic check "IF my bank balance is at least the amount of money I want to withdraw THEN let me withdraw my money".
X is the predicate "My bank balance is at least the amount of money I want to withdraw", or written more simply: bankBalance >= withdrawalAmount. If this inequality evaluates to true, bankBalance is at least equal to withdrawalAmount and the ATM will dispense my withdrawal amount.
We may also want to do a bit more than that. We might hopefully also want to check that the pin we entered is correct before we are allowed to withdraw. This gives the following implication. "IF bankBalance >= withdrawalAmount AND accountPin = enteredPin THEN withdrawMoney()". The lefthand side of the implication contains two predicates, P - bankBalance >= withdrawalAmount, and Q - accountPin = enteredPin. Together these two predicates must evalute to true before the money is withdrawn. Logic is easily reprsented by true tables and the AND truth table looks like the figure below.
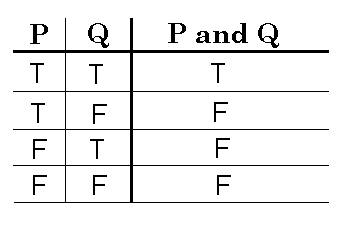 Here we can see that the only way for the money to come out is if both statements are true. This is easy to understand if we use the banking statement.
Here we can see that the only way for the money to come out is if both statements are true. This is easy to understand if we use the banking statement.
However, a conversation on the Internet (oh no...) I had today, followed by a conversation I had with my wife, leads me to believe that people actually think different to this (oh no!)
For example: If I said "Get all the plates that are blue and green", my wife would come back with all plates that are blue and all plates that are green, this includes any plate that has blue and green on it. What I meant by that statement is that for a plate to be returned the plate must have both green and blue on it, that is both P and Q. If I wanted what my wife did I'd have said "Please get all the plates that have blue and all the plates that have green, as well as any plate that has both on them". Or using predicate logic I could have said "Please get me all the blue or green plates". She would get any plates that have blue, plates that have green, plates that blue and green, but not plates that didn't have either blue or green. You can see this result in an OR truth table.
I guess thinking about the use of a conjunction ("and") in a different context, you can say "Go for a ride and a swim" and common sense says that doesn't mean go for a ride and a swim at the same time. But what the person really means is "Go for a ride and then a swim". Which is actually an implication, If Ride THEN Swim, where you can go for a swim only if you have been for a ride. Note, it is technically possible to try and go for a ride and a swim at the same time. Hilarity will ensue.
The point I'm attempting to make is programmers spend a long time in a many different types of languages (and grammars) and it changes the way we think. Although, basic predicate logic is not a langauge, so this whole post is not really about languages and more about collequal language I guess.